Exchange symmetry
Exchange symmetry is derived from a fundamental postulate of quantum statistics, which states that no observable physical quantity should change after exchanging two identical particles. It states that because all observables are proportional to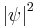 
for a system of identical particles, the wave function 
must either remain the same or change sign upon such an exchange.
Because the exchange of two identical particles is mathematically equivalent to the rotation of each particle by 180 degrees (and so to the rotation of one particle's frame by 360 degrees) [1] , the symmetric nature of the wave function depends on the particle's spin after the rotation operator is applied to it. Integer spin particles do not change the sign of their wave function upon a 360 degree rotation—therefore the sign of the wave function of the entire system does not change. Semi-integer spin particles change the sign of their wave function upon a 360 degree rotation (see more in spin-statistics theorem).
Particles for which the wave function does not change sign upon exchange are called bosons, or particles with a symmetric wave function. The particles for which the wave function of the system changes sign are called fermions, or particles with an antisymmetric wave function.
Fermions therefore obey different statistics (called Fermi-Dirac statistics) than bosons (which obey Bose-Einstein statistics). One of the consequences of Fermi-Dirac statistics is the exclusion principle for fermions—no two fermions can share the same quantum state (in other words, the wave function of two fermions in the same state is zero). This in turn results in degeneracy pressure for fermions—the strong resistance of fermions to compression into smaller volume. This resistance gives rise to the “stiffness” or “rigidity” of ordinary atomic matter (as atoms contain electrons which are fermions).